INTRODUCCIÓN
En el presente trabajo se estudia las vigas con tres o mas apoyos, dos o mas tramos, y que, por tanto, disponen de uno o mas apoyos redundantes en los que las reacciones no pueden determinarse por las ecuaciones de la Estática.
En el método de los tres momentos se comienza obteniendo una relación de tipo general entre los momentos flexionantes en tres secciones cualesquiera de la viga, relación que se llama Ecuación de los tres momentos, y que se escribe fácilmente aplicando los teoremas de las áreas de momentos.
La Ecuación de los tres momentos fue desarrollada por el ingeniero francés Clapeyron en 1857. Esta ecuación relaciona los momentos internos de una viga continua en tres puntos de soporte con las cargas que actúan en los soportes. Por aplicación sucesiva de esta ecuación a segmentos de la viga se obtiene un conjunto de ecuaciones que pueden resolverse simultáneamente para los momentos internos desconocidos en los soportes.
Las aplicaciones de esta ecuación son numerosas, como determinar las deformaciones y reacciones redundantes en cualquier tipo de vigas, en particular en las vigas continuas.
Se terminará el presente con algunos ejercicios de aplicación para la teoría expuesta.
GENERALIDADES.-
Objetivos:
Limitaciones:
- Solo aplicación del método en vigas continúas.
Glosario de Términos:
- Se darán en el desarrollo del Marco teórico del trabajo.
MARCO TEÓRICO.-
ECUACION DE LOS TRES MOMENTOS
Sea una viga sometida a una carga cualquiera que soporte en forma arbitraria.
A esta viga la hemos cortado en 3 puntos cualesquiera 1, 2,3, además hemos reemplazados los efectos de cargas y fuerzas a la derecha o izquierda de cada sección de corte por la fuerza cortante y el momento flector.
La longitud de los tramos serán y los momentos flectores serán las fuerzas cortantes acompañan a la misma teniendo en cuenta que cada extremo se encuentra perfectamente en equilibrio
De esta manera hemos transformado a cada uno de estos tramos en una viga solamente apoyada con 2 estados de cargas que sabremos distinguir, por un lado las cargas reales en un tramo y por otro los pares aplicados en sus extremos
.JPG)
.JPG)
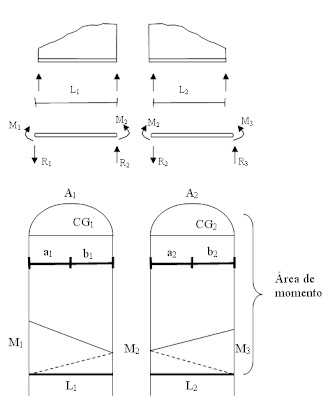
En el esquema se presenta en forma genérica los diagramas de momentos debido a las cargas cortantes en cada tramo y debido a los momentos generados en los extremos de cada corte.
La tangente trazada a la elástica en el punto 2 determina la desviación tangencial 1/2 y 3/2 respectivamente y la recta trazada por dos paralelas a la posición inicial a la viga que por comodidad supondremos que la horizontal determina la altura de los puntos 1 y 3 respecto al punto 2.
 Como se puede observar el diagrama de momento flector se le ha descompuesto en el área y áreas triangulares en que se descomponen el área trapezoidal producida por los 2 pares extremos. Lo mismo sucede en el área de donde podemos concluir que la desviación 12 esta dado por cada uno con su mismo brazo.
Como se puede observar el diagrama de momento flector se le ha descompuesto en el área y áreas triangulares en que se descomponen el área trapezoidal producida por los 2 pares extremos. Lo mismo sucede en el área de donde podemos concluir que la desviación 12 esta dado por cada uno con su mismo brazo. Regla de Signos:
En la deducción de la Ecuación General de los Tres Momentos se ha hecho la hipótesis de que los momentos flexionantes en los tres puntos son positivos y que los puntos 1 y 3 estaban situados por encima del punto 2. Si el momento flexionante en cualquiera de los puntos es negativo habrá que considerarlo con signo menos al sustituir su valor en la ecuación. Recíprocamente, si al resolver la ecuación sale un valor negativo para cualquiera de los momentos, es que en realidad es negativo. Las alturas h1 y h3 son positivas si los puntos si los puntos 1 y 3 quedan por encima del 2, y son negativos, o se obtendrán con signo menos, si el punto 1 o el 3 están por debajo del punto 2.
Regla de Signos:
En la deducción de la Ecuación General de los Tres Momentos se ha hecho la hipótesis de que los momentos flexionantes en los tres puntos son positivos y que los puntos 1 y 3 estaban situados por encima del punto 2. Si el momento flexionante en cualquiera de los puntos es negativo habrá que considerarlo con signo menos al sustituir su valor en la ecuación. Recíprocamente, si al resolver la ecuación sale un valor negativo para cualquiera de los momentos, es que en realidad es negativo. Las alturas h1 y h3 son positivas si los puntos si los puntos 1 y 3 quedan por encima del 2, y son negativos, o se obtendrán con signo menos, si el punto 1 o el 3 están por debajo del punto 2.
Vigas Continuas
Cuando se trabajan con vigas con más de un tramo, las reacciones no pueden ser calculadas estáticamente. Una forma de resolverlas es aplicando el Teorema de los Tres Momentos, el cual puede ser utilizado también para resolver vigas de un solo tramo. Esta ecuación puede ser expresada de la siguiente manera:
Estos tipos básicos de carga pueden combinarse para obtener tipos más complejos, sumándose o restándose.
Si se va a trabajar con más de dos tramos, deben escribirse una ecuación de Tres Momentos por cada par de tramos consecutivos. Por ejemplo:
En este caso tendríamos 3 ecuaciones con 5 incógnitas (M1, M2, M3, M4 y M5). Generalizando, siempre vamos a tener dos incógnitas más que las ecuaciones de Tres Momentos que vamos a construir. Pero los momentos en estos extremos pueden ser hallados de acuerdo a los siguientes criterios:
1º Si tenemos un apoyo simple, el momento en dicho extremo será igual a cero. Para el diagrama de arriba, M1 = 0 y M5 = 0.
2º Si tenemos un empotramiento, se puede construir una ecuación adicional de Tres Momentos, creando un tramo virtual en el que todos los valores sean iguales a cero. Para el diagrama de arriba, si suponemos que el apoyo 5 es un apoyo empotrado, podríamos escribir la siguiente ecuación de Tres Momentos, en donde todos los términos con subíndice cero valen cero:
 3º Si tenemos un voladizo, el momento en tal extremo seguirá valiendo cero. Además, el momento siguiente al de dicho extremo será igual a la suma de los productos de las cargas por su brazo de palanca a este último apoyo.
3º Si tenemos un voladizo, el momento en tal extremo seguirá valiendo cero. Además, el momento siguiente al de dicho extremo será igual a la suma de los productos de las cargas por su brazo de palanca a este último apoyo.
Aplicando el Teorema de los Tres Momentos es fácil obtener los momentos flectores en cada apoyo. Hallar las reacciones en cada apoyo es igualmente sencillo, utilizando la siguiente fórmula, para cada tramo:
Posteriormente, las reacciones equivalentes de cada tramo se suman. Por ejemplo:


.JPG)






No hay comentarios:
Publicar un comentario